In this [post](https://www.sabrina.dev/p/chatgpt4o-vs-math), Sabrina Ramonov uses the roll of tape math problem to test the performance of LLMs in solving less known math problems.
The problem was created by Neil Fraser and can be stated as:
```
There is a roll of tape. The tape is 100 meters long when unrolled. When rolled up, the outer diameter is 10 cm, and the inner diameter is 5 cm. How thick is the tape?
```
The following image illustrates the problem:
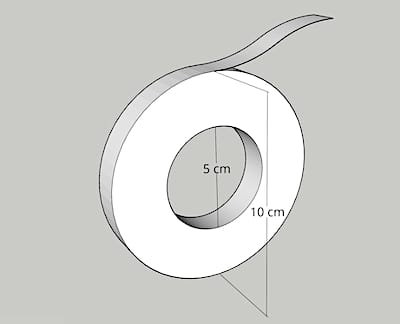
The solution is thickness $T=0.00589$ cm.
The Bing Copilot (GPT-4) is not able to solve the problem:
> [!Bing Copilot]-
> To calculate the thickness of the tape, we can use the following formula:
> $
> \text{Thickness} = \frac{\text{Volume}}{\text{Area}}Thickness=AreaVolume
> $
> First, let’s find the volume of the rolled tape. The outer diameter is 10 cm, so the radius is half of that, which is 5 cm. The inner diameter is 5 cm, so the inner radius is also 5 cm. The length of the tape is 100 meters, which is equivalent to 10000 cm.
>
> 1. Calculate the volume of the rolled tape:
>
> - Volume = π × (outer radius)^2 × length
> - Volume = π × (5 cm)^2 × 10000 cm = 785398 cm³
> 2. Next, find the area of the rolled tape:
>
> - Area = π × [(outer radius)^2 - (inner radius)^2]
> - Area = π × [(5 cm)^2 - (5 cm)^2] = 0 cm²
> 3. Now, calculate the thickness:
>
> - Thickness = Volume / Area
> - Thickness = 785398 cm³ / 0 cm² (Note: Since the area is zero, the thickness is undefined.)
>
> It seems that the thickness cannot be determined based on the given information.
But GPT-4o can:
> [!GPT-4o]-
> To determine the thickness of the tape, we need to calculate the cross-sectional area of the tape when it is unrolled and then relate it to the area of the rolled tape.
>
> First, let's calculate the cross-sectional area of the tape when it is rolled up. The tape forms a cylindrical shell, with an outer radius \( R = 5 \) cm (since the outer diameter is 10 cm) and an inner radius \( r = 2.5 \) cm (since the inner diameter is 5 cm).
>
> The area of the rolled tape, as a cylindrical shell, can be found by subtracting the area of the inner circle from the area of the outer circle:
> $
> A = \pi R^2 - \pi r^2 = \pi (R^2 - r^2)
> $
> Substitute \( R = 5 \) cm and \( r = 2.5 \) cm:
> $
> A = \pi (5^2 - 2.5^2) = \pi (25 - 6.25) = \pi \times 18.75 \, \text{cm}^2
> $
>
> This area represents the total cross-sectional area of the tape when it is rolled up.
>
> Next, we know the tape is 100 meters (10,000 cm) long. The thickness \( t \) of the tape is the width of this cross-sectional area divided by the length of the tape.
>
> If the tape is unrolled, it forms a long, thin rectangular shape with a width equal to its thickness \( t \) and length 10,000 cm. The area of this rectangle is also the same cross-sectional area we calculated earlier:
> $
> \text{Area} = \text{length} \times \text{thickness}
> $
>
>
> $\pi \times 18.75 \, \text{cm}^2 = 10,000 \, \text{cm} \times t
>
> $
>
> Solving for \( t \):
> $
> t = \frac{\pi \times 18.75}{10,000}
> $
>
> $
> t = \frac{18.75 \pi}{10,000}
> $
>
> Using \(\pi \approx 3.14159\):
> $
> t = \frac{18.75 \times 3.14159}{10,000} \approx \frac{58.9044}{10,000} \approx 0.00589044 \, \text{cm}
> $
>
> Therefore, the thickness of the tape is approximately:
> $
> \boxed{0.059} \, \text{mm}
> $
## Using chain of thought
```
Take a deep breath and work on this problem step-by-step: <There is a roll of tape. The tape is 100 meters long when unrolled. When rolled up, the outer diameter is 10 cm, and the inner diameter is 5 cm. How thick is the tape?>
```