The mel spectrum is a frequency representation where the frequencies are scaled to better match the human perception of sound. This scaling is accomplished using the [[mel frequency scale]], which is a non-linear transformation of frequency that emphasizes lower frequencies more than higher frequencies. The resulting mel spectrum is a series of frequency bands that are evenly spaced on the Mel scale, rather than on the linear frequency scale. This makes it easier to analyze and compare different sounds based on their perceived tonal characteristics, rather than just their raw frequency content. To compute a mel frequency spectrum, a series of overlapping triangle filters are applied to the magnitudes of the FFT spectrum. Each FFT value is multiplied by its corresponding value in each triangle filter. The resulting values are then summed up for each filter, creating a series of energy values in each mel frequency band. This process is often referred to as "mel filtering". 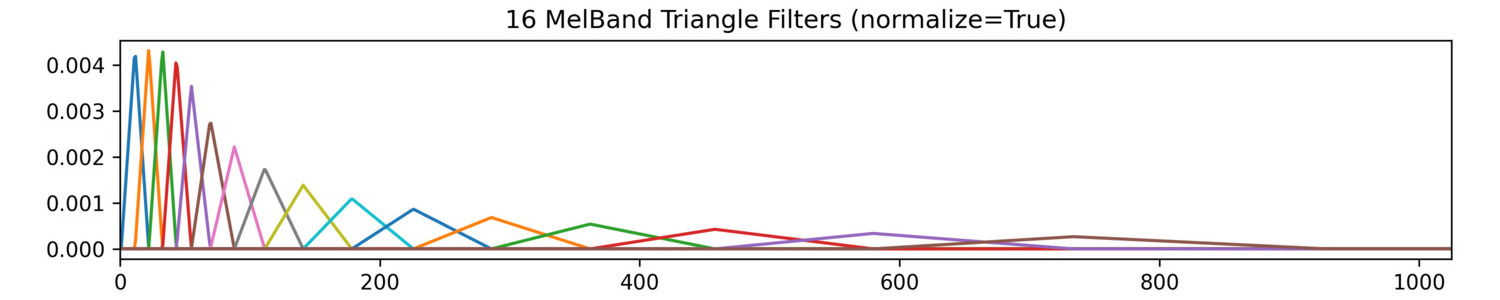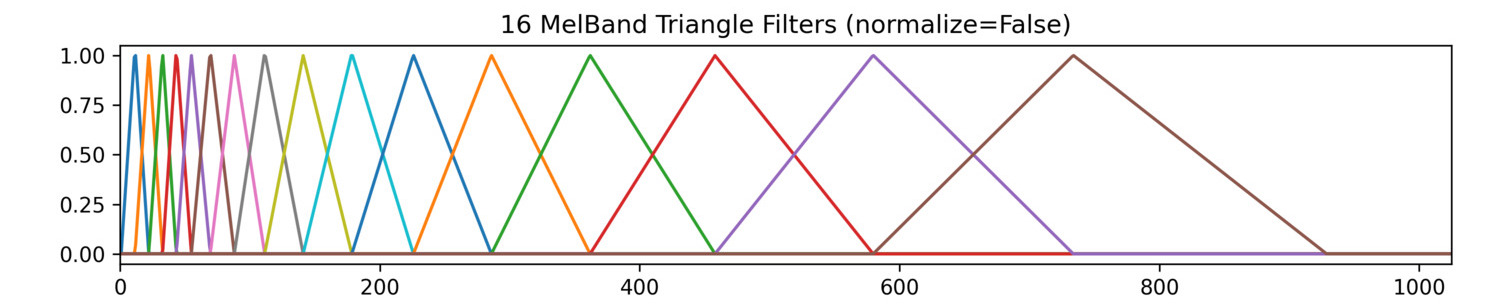The amplitudes of the filters can be normalized so that each triangle has the same area: [](https://learn.flucoma.org/reference/melbands/norm=True.jpg) When the amplitudes are not normalized, all the filters have the same amplitude: [](https://learn.flucoma.org/reference/melbands/norm=False.jpg) To represent a signal in a mel scale, one needs to define the number of filters in which to divide the frequency range. The number of filters used can vary depending on the specific application and the characteristics of the signal being analyzed. Typically, between 20 and 40 filters are used, with higher numbers of filters providing more detailed information about the frequency content of the signal. The mel-frequency spectrum is defined as: $ M(r) = \frac{1}{A_{r}} \sum_{k=L_{r}}^{U_{r}} |V_{r}(k) X(k)| $ where $X(k)$ is the [[discrete Fourier transform (DFT)]] of the signal, $V_{r}(k)$ is the triangular weighting function for the 𝑟-th filter, $L_{r}$ and $U_{r}$ are the lower and upper indices of the frequencies of the triangular filter, $A_r$ is the amplitude normalization factor of the filter. To make that a perfectly flat Fourier spectrum will also produce a flat Mel-spectrum it is necessary the normalization factor of: $ A_{r} = \sum_{k=L_{r}}^{U_{r}} |V_{r}(k)|^2 $